Codeforces Round #811 (Div. 3)

A.Everyone Loves to Sleep

题目大意

​ 给定一个睡觉时间 H:MH:M 和 nn 个闹钟 h:mh:m， 问能睡多久

分析

​ 时间化为分钟，做差，注意闹钟时间小于睡觉时间 + 24∗6024*60 后再做差

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
struct node{
    int H,M;
};
void solve(){
    int n,h,m;
    cin>>n>>h>>m;
    vector<node> a(n+1);
    forr(i,1,n) cin >> a[i].H >> a[i].M;
    int t = h*60+m;
    int res = inf;
    forr(i,1,n){
        int nt = a[i].H*60+a[i].M;
        if(nt < t) nt += 24*60;
        res = min(res,nt-t);
        
    }
    cout << res/60 <<" "<< res%60 << endl;
}

B.Remove Prefix

题目大意

​ 最少删多少前缀剩下的数组元素各相同

分析

​ 记录一个元素出现的最后位置 mp[a[i]]mp[a[i]]，遍历数组 ii , 若 i !=mp[a[i]]i \ != mp[a[i]]，

记录答案为 res=ires = i ，输出 resres

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void solve(){
    int n;cin>>n;
    vector<int> a(n+1);
    map<int,int> mp;
    forr(i,1,n) cin >> a[i],mp[a[i]] = i;


    int f = 0;
    forr(i,1,n){
        if(mp[a[i]] != i){
            f = i;
        }
    }
    
    cout << f << endl;
}

C.Minimum Varied Number

题目大意

​ 输出一个每一位都不相同的最小 nn 使得 nn 每一位相加等于 ss

分析

​ 观察到 s<=45s <= 45 考虑达标

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
map<int, int> mp;
void init()
{
    mp[1] = 1;
    mp[2] = 2;
    mp[3] = 3;
    mp[4] = 4;
    mp[5] = 5;
    mp[6] = 6;
    mp[7] = 7;
    mp[8] = 8;
    mp[9] = 9;
    mp[10] = 19;
    mp[11] = 29;
    mp[12] = 39;
    mp[13] = 49;
    mp[14] = 59;
    mp[15] = 69;
    mp[16] = 79;
    mp[17] = 89;
    mp[18] = 189;
    mp[19] = 289;
    mp[20] = 389;
    mp[21] = 489;
    mp[22] = 589;
    mp[23] = 689;
    mp[24] = 789;
    mp[25] = 1789;
    mp[26] = 2789;
    mp[27] = 3789;
    mp[28] = 4789;
    mp[29] = 5789;
    mp[30] = 6789;
    mp[31] = 16789;
    mp[32] = 26789;
    mp[33] = 36789;
    mp[34] = 46789;
    mp[35] = 56789;
    mp[36] = 156789;
    mp[37] = 256789;
    mp[38] = 356789;
    mp[39] = 456789;
    mp[40] = 1456789;
    mp[41] = 2456789;
    mp[42] = 3456789;
    mp[43] = 13456789;
    mp[44] = 23456789;
    mp[45] = 123456789;
}
void solve()
{
    int s;cin>>s;
    cout << mp[s] << endl;
}

D.Color with Occurrences

题目大意

​ 给定一个模板串和 nn 个匹配串,问最少需要几个串匹配串(可以多次使用)，把整个模板串覆盖

分析

​ 观察到 nn 和 ∣s∣\left | s \right | $<= 10 $ ,先对每个匹配串暴力匹配模板串记录匹配到模板串的范围，转化为求最小区间覆盖问题

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
struct node{
    int first,second;
    int id;
};

bool cmp(node &a,node &b){
    if(a.first == b.first) return a.second > b.second;
    return a.first < b.first;
}
void solve(){
    string str;
    cin>>str;
    int n;cin>>n;
    vector<node> p;
    int id = 0;
    forr(i,1,n){
        string s;cin>>s;
        if(s.size() > str.size()) continue;
        int len = s.size();
        for(int j = 0;j + len -1 < str.size();j++){
            int l = j,r = 0;
            while(str[l] == s[r] && l < str.size() && r < s.size()) l++,r++;
            if(r == s.size()){ 
                p.push_back({j,j+len-1,i});
            }
        }
    }

    if(p.size() == 0){
        cout <<"-1" << endl;
        return;
    }
    vector<pll> ans;

    int nn = p.size()-1;
    sort(p.begin(),p.end(),cmp);
    // forr(i,0,p.size()-1){
    //     cout << p[i].first <<" "<< p[i].second << endl;
    // }
    
    int mr;
    int l = p[0].first, r = p[0].second;
    mr = r;
    if(l > 0){
        cout << "-1" << endl;
        return;
    }
    ans.push_back({p[0].id,p[0].first+1});
    int res = 1;
    int cnt = 1;
    
    while(cnt <= nn && r < str.size()-1){
        if(p[cnt].first > r+1){
            cout << -1 << endl;
            return;
        }
        node t;
        bool flag = 0;
        while(p[cnt].first <= r+1 && cnt <= nn && mr < str.size()-1){
            //mr = max(mr,p[cnt].second);
            if(mr < p[cnt].second){
                flag = 1;
                mr = p[cnt].second;
                t = p[cnt];
            }
            cnt++;
        }
        r = mr;
        if(flag) ans.push_back({t.id,t.first+1});
        res++;
    }

    if(mr < str.size()-1){
        cout << -1 << endl;
        return ;
    }
    else cout << res << endl;

    for(auto k:ans){
        cout << k.first <<" "<< k.second << endl;
    }
    ans.clear();
}

E.Add Modulo 10

题目大意

​ 给定一个数组 aa，每次可以进行一个操作使某个位置 $ a_i = a_i + a_i \ mod \ 10$, 问进行这样的操作是否可以使得数组 aa 的所有元素相同

分析

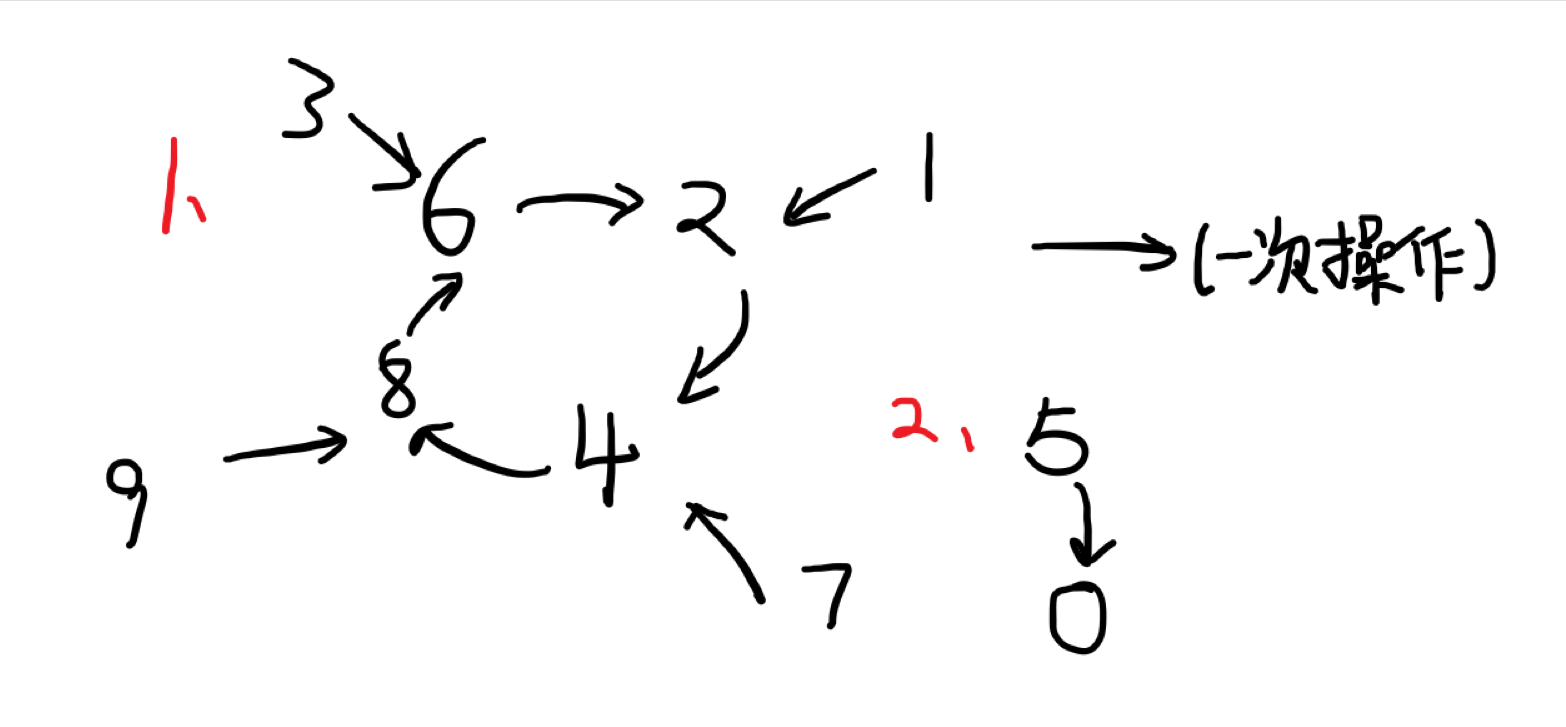
​ 对与 $ a_i $ 进行多次操作，会发现 $ a_i $ 的个位会出现循环，循环如下

image-20220803232401108

一共两种循环，并且 8→68 \rightarrow 6 都会进行一次进位

egeg

1. $ \ 14 \rightarrow 18,18 \rightarrow 26$  
2. $22 \rightarrow 24,24 \rightarrow 28,28 \rightarrow 36 $

并且发现对于 aia_i 若 $ t = a_i \ mod \ 10 = 6 $

则 $ k = a_i / 10 $， $ k $ 的奇偶性不变

$ eg $

1. $26 \  -....-> 46$
2. 36 $- ... -> 56 $

综上规律可以得出结论

1. 如果出现两种循环一定是  $no$
2. 对于第一种循环
  	1. 先把个位为$ 1 \ 3\  7\  9$  的 $a_i$,进行一次操作后，进入第一个循环
  	2. 记录 $a_i$  第一次进入$6$ 时 $k$ 的奇偶性
  	3. 若 $a$ 的奇偶性不相同,输出 $no$ ,反之 $yes$
3. 对于第二种循环
	1. 把所有各位为 $5$ 的进行一次操作
	2. 若所有 $a_i$ 不相同,输出 $no$ ,反之 $yes$

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
void solve(){
    int n;cin>>n;
    vector<int> a(n+1);
    int x = 0,y = 0;
    int mx = -inf;
    forr(i,1,n){
        cin >> a[i];
        mx = max(mx,a[i]);
        int k = a[i]%10;
        if(a[i]%10 == 0 || a[i]%10 == 5) x++;
        else y++;
        if(k==1||k==7||k==9||k==3){
            a[i] += k;
        }
    } 
    if(x&&y){
       cout << "no"<<endl;
        return;
    }
    map<int,int> mp;
    if(!x){
        // cout << 1 << endl;
        int l = 0,r = 0;
        forr(i,1,n){
            int t = a[i] % 10;
            int q = a[i]/10;
            map<int,int> mp;
            if(t == 6){
                if(q&1) l++;
                else r++;
            } 
            else {
                q++;
                if(q&1) l++;
                else r++;
            }
        }

        if(l && r){
            cout <<"no" << endl;
            return;
        }
        else {
            cout <<"yes" << endl;
            return;
        } 

    }
    else{
        forr(i,1,n){
            int t = a[i]%10;
            if(t == 5) a[i] += t;
            mp[a[i]]++;
        }
        if(mp.size() > 1){
            cout <<"no" << endl;
        }
        else cout <<"yes" << endl;
    }
}

G.Path Prefixes

题目大意

​ 一颗有 nn 个结点的有根树，根为 11, 每条边有两个权值 a,ba,b

​ 问对于顶点 ii , 规定 wawa 为 ii 到顶点 权值 aa 的和, $ wb $ 同理

​ 问 对于顶点 ii 最大的前缀长度使得 wa>=wbjwa >= wb_j jj 为 ii到11 路径上点顶点

分析

​ 很显然对于顶点$ i$ 想要找到顶点 jj ,满足 wa>=wbjwa >= wb_j

​ 只需要二分一下 wbwb 找到 jj 即可

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
int n;
struct node{
    int to,ne;
    int a,b;
}e[200005];
int h[200005],cnt = 1;
void add(int u,int v,int w1,int w2){
    e[++cnt] = {v,h[u],w1,w2};
    h[u] = cnt;
}
ll wa[200005],wb[200005];
int res[200005];
vector<ll> t;
void dfs(int u,int fa){
    for(int i = h[u];i;i = e[i].ne){
        int v =e[i].to;
        if(v == fa) continue;
        wa[v] = wa[u] + e[i].a;
        wb[v] = wb[u] + e[i].b;
        t.push_back(wb[v]);
        res[v] = upper_bound(t.begin(),t.end(),wa[v]) - t.begin();
        dfs(v,u);
        t.pop_back();
    }
}



void solve(){
    cin >> n;
    forr(i,1,n){
        h[i] = 0;
        cnt = 1;
        wa[i] = wb[i] = 0;
    }
    forr(i,2,n) {
        int x;cin>>x;
        int l,r;cin>>l>>r;
        add(x,i,l,r);
    }

    dfs(1,0);
    forr(i,2,n) cout << res[i] <<" \n"[i==n];
}