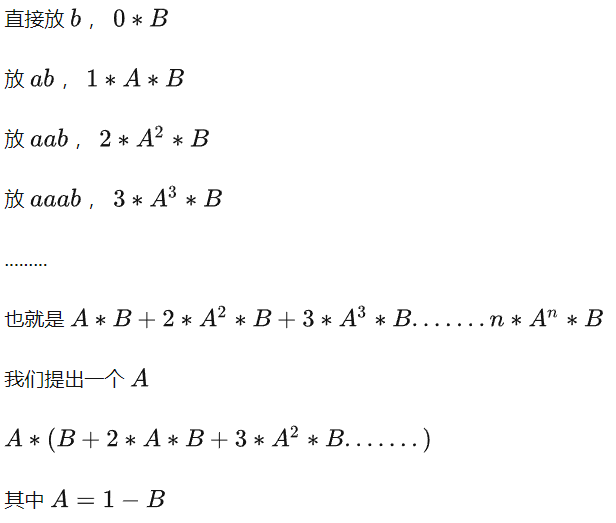题目大意

分析

考虑 $f[i][j]$ 表示有 $i$ 个 $a$ 和 $j$ 个匹配的 $ab$ 的期望

容易想到转移

$f[i][j] = pa/(pa+pb)* f[i+1][j] + pb/(pa+pb)*f[i][j+i]$

因为单独一个 $b$ 无法对 $ab$ 产生贡献，所以最后的答案是 $f[1][0]$

现在要考虑如果前面都是 $a$ 的情况要如何处理

如果当 $i+j >= k$ 时，只要再放一个 $b$ 就可以了

那么就是在考虑第一次放 $b$ 后的子序列 $ab$ 期望个数

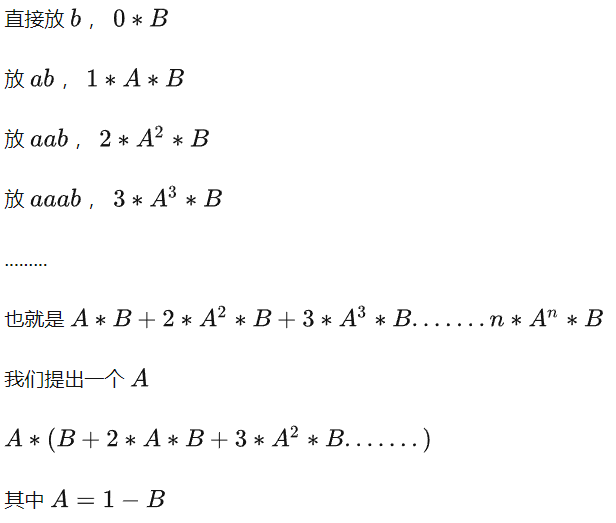
因为不好确定 $dp$ 方向,所以进行记忆化搜索

Code

const int mod = 1e9+7;
template<int T>
struct ModInt {
    const static int MD = 1e9+7;
    int x;
    ModInt(ll x = 0) : x(x % MD) {}
    int get() { return x; }
    ModInt operator + (const ModInt &that) const { int x0 = x + that.x; return ModInt(x0 < MD ? x0 : x0 - MD); }
    ModInt operator - (const ModInt &that) const { int x0 = x - that.x; return ModInt(x0 < MD ? x0 + MD : x0); }
    ModInt operator * (const ModInt &that) const { return ModInt((long long)x * that.x % MD); }
    ModInt operator / (const ModInt &that) const { return *this * that.inverse(); }
    void operator += (const ModInt &that) { x += that.x; if (x >= MD) x -= MD; }
    void operator -= (const ModInt &that) { x -= that.x; if (x < 0) x += MD; }
    void operator *= (const ModInt &that) { x = (long long)x * that.x % MD; }
    void operator /= (const ModInt &that) { *this = *this / that; }
    ModInt inverse() const {
        int a = x, b = MD, u = 1, v = 0;
        while (b) {
            int t = a / b;
            a -= t * b; std::swap(a, b);
            u -= t * v; std::swap(u, v);
        }
        if (u < 0) u += MD;
        return u;
    }
};
typedef ModInt<mod> mint;
mint pa,pb;
int k;

bool st[1005][1005];
mint f[1005][1005];

mint dfs(int i,int j){
    if(st[i][j]) return f[i][j];
    st[i][j] = 1;
    if(i+j >= k) return f[i][j] = (pa/pb+i+j);
    return f[i][j] = (pa/(pa+pb))*dfs(i+1,j) + (pb/(pa+pb))*dfs(i,j+i);
}
signed main()
{
    cin >> k >> pa.x >> pb.x;
    cout << dfs(1,0).get()  << endl;
    return 0;
}

mint 板子

template<int T>
struct ModInt {
    const static int MD = 1e9+7;
    int x;
    ModInt(ll x = 0) : x(x % MD) {}
    int get() { return x; }
    ModInt operator + (const ModInt &that) const { int x0 = x + that.x; return ModInt(x0 < MD ? x0 : x0 - MD); }
    ModInt operator - (const ModInt &that) const { int x0 = x - that.x; return ModInt(x0 < MD ? x0 + MD : x0); }
    ModInt operator * (const ModInt &that) const { return ModInt((long long)x * that.x % MD); }
    ModInt operator / (const ModInt &that) const { return *this * that.inverse(); }
    void operator += (const ModInt &that) { x += that.x; if (x >= MD) x -= MD; }
    void operator -= (const ModInt &that) { x -= that.x; if (x < 0) x += MD; }
    void operator *= (const ModInt &that) { x = (long long)x * that.x % MD; }
    void operator /= (const ModInt &that) { *this = *this / that; }
    ModInt inverse() const {
        int a = x, b = MD, u = 1, v = 0;
        while (b) {
            int t = a / b;
            a -= t * b; std::swap(a, b);
            u -= t * v; std::swap(u, v);
        }
        if (u < 0) u += MD;
        return u;
    }
};
typedef ModInt<mod> mint;