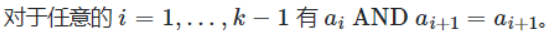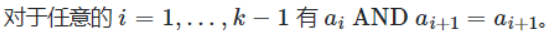与

题目大意

分析

按位考虑 $a_i$

考虑 $dp[i][j]$ 表示为考虑到第 $i$ 位总和为 $j$ 的方案数

为满足要求

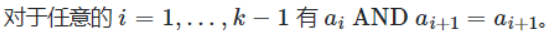
会发现对于第 $i$ 位来说 $1$ 的个数都是连续的,我们可以枚举第 $i$ 位有 $k$ 个 $1$

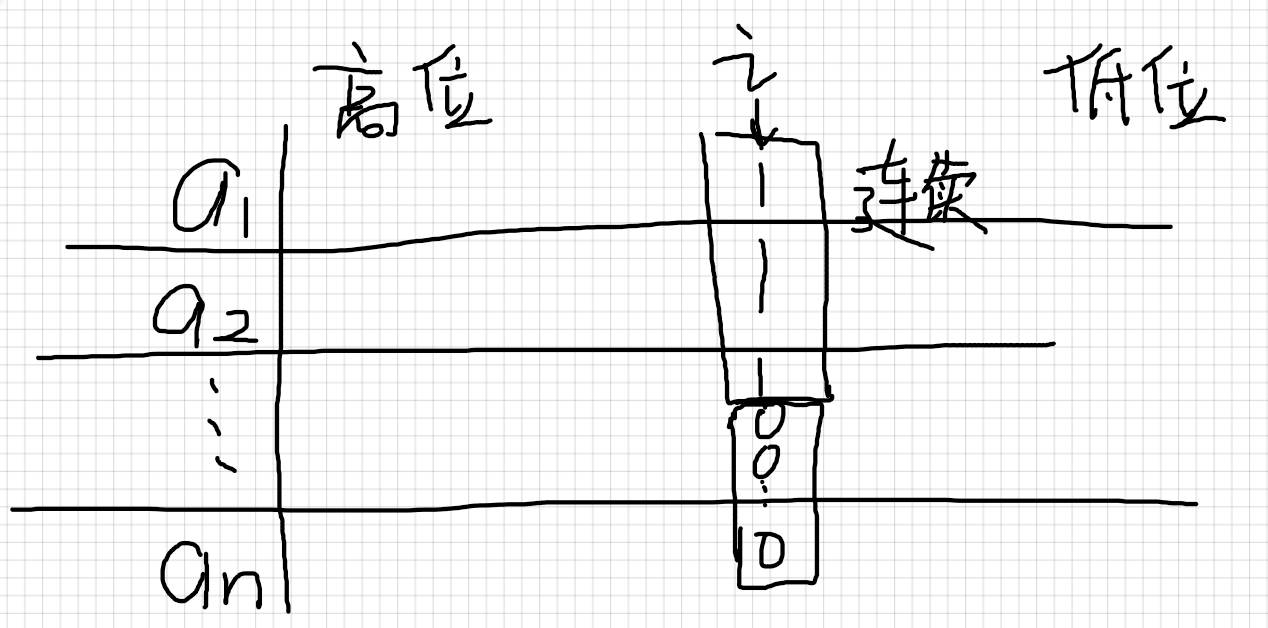
那么转移方程为

从高位到低位考虑

f[cnt+1][0] = 1;
for(int i = cnt+1;i > 0;i--){
    for(int j = 0;j <= n;j++){
        for(int o = 0;o <= k;o++){
            if(j + o*(1LL<<(i-1)) > n) break; 
            f[i-1][j+((1LL<<(i-1)))*o] = (f[i-1][j+((1LL<<(i-1)))*o] + f[i][j])%mod; 
        }
    }
}

时间复杂度$O(n^{2} log^n)$

Code

int n,k;
int f[32][10005];
signed main()
{
    cin >> k >> n;
    int cnt = 0;
    int t = n;
    while(t){
        cnt++;
        t >>= 1;
    }
    cnt--;
    f[cnt+1][0] = 1;
    for(int i = cnt+1;i > 0;i--){
        for(int j = 0;j <= n;j++){
            for(int o = 0;o <= k;o++){
                if(j + o*(1LL<<(i-1)) > n) break; 
                f[i-1][j+((1LL<<(i-1)))*o] = (f[i-1][j+((1LL<<(i-1)))*o] + f[i][j])%mod; 
            }
        }
    }

    cout << f[0][n] << endl;
    return 0;
}