题目大意

题目大意

分析

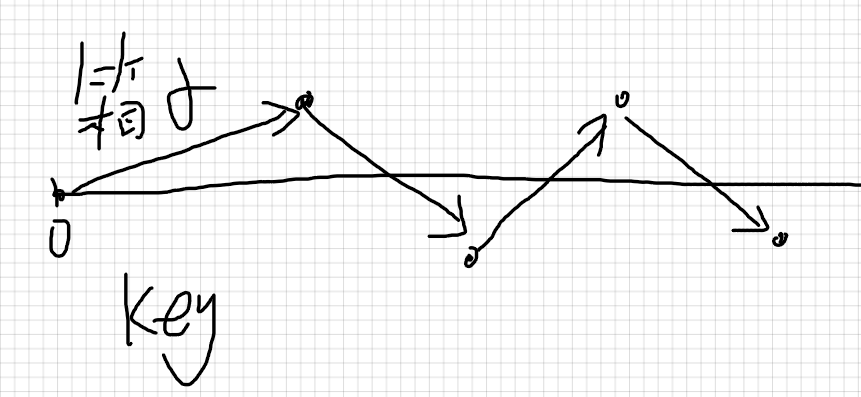
分析

我们对箱子和钥匙按顺序连线

会发现有些边会可能会经过三次

那些边会经过三次呢？

从起点开始到一点 ii

如果钥匙的数量小于箱子的数量，那么这一点 ii 后面的那条边就要走 33 次

基于这一点我们可以找出所有需要走 33 次的边

对边权做一个前缀和

如何找到答案呢？

答案可以基于这个策略找到：

我们可以枚举最后一个被打开的宝箱的位置 pp

对于 p 前则会贡献 sum[p]sum[p]

对于 pp 后 我们看有没有需要走 3 次的边，如果有就从 pp 走到头再走回 pp,否则就直接走到头

时间复杂度 O(n)O(n)

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
signed main()
{
    int n;cin >> n;
    vector<int> b(n+1),c(n+1);
    vector<pair<int,int>> a;
    for(int i = 1;i <= n;i++) cin >> b[i],a[i],a.push_back({b[i],1});
    for(int i = 1;i <= n;i++) cin >> c[i],a.push_back({c[i],-1});

    sort(a.begin(),a.end());
    int len = a.size();
    vector<int> f(a.size(),0);
    int cnt = a[0].second;
    vector<int> st(a.size());
    for(int i = 1;i < a.size();i++){
        st[i] = st[i-1];
        if(cnt > 0) f[i] = 1,st[i]++;
        cnt += a[i].second;
    }

    // for(int i = 1;i < len;i++) cout << st[i] << endl;
    vector<int> sum(a.size());
    sum[0] = a[0].first;
    for(int i = 1;i < a.size();i++){
        if(f[i])    sum[i] = sum[i-1] + (a[i].first - a[i-1].first)*3;
        else sum[i] = sum[i-1] + (a[i].first - a[i-1].first);
    }

    
    int res = 1e18;
    for(int i = 0;i < a.size();i++){
        if(a[i].second == 1){
            int t = a[len-1].first - a[i].first;
            if(st[i] != st[len-1]) t = t << 1; 
            res = min(res,sum[i]+t);
        }
    }
    cout << res << endl;
    return 0;
}